We'll introduce the principle hero of our story: the exponential function, and dive deeper into its definition and the implications thereof. We'll also see how Euler's formula entwines the exponential function with our principle supporting actors, the trigonometric functions. What is e to the x, the exponential function. Well, of course it's a function. Hence we can plot the graph of this function and consider what the output e to the x looks like for various inputs x.
But how do we compute some of these outputs? Let's say for an irrational input, like pi. How would we even make sense of exponentiating an imaginary or a complex number. Is it possible to give meaning or sense to exponentiating an operator like the derivative, or more unusual objects that you may have seen such as matrices. Well, we won't answer all of those questions today, but let's recall a few facts about the exponential function. Certain algebraic properties are manifest and well known to us. From your prior exposure to calculus, you should have seen some differential and integral properties. e to the x is that remarkable function that is its own derivative. And thus, it is its own integral, up to the constant of integration. There's one other fact that we need to move forward, and that is Euler's formula that tells us something about exponentiating a complex input, namely e to the ix is cosine of x plus i times sine of x. None of these properties however, tell us what e to the x really means.
This is what e to the x is and means. We define e to the x as 1 plus x, plus one half x squared, plus one sixth x cubed, plus one 24th x to the fourth, plus one over 120 times x to the fifth and this keeps on going and going. Where do these numbers come from? What do they mean? Well, another way to write this is using
factorial notation. That e to the x is 1 + x + x squared over 2 factorial + x cubed over 3 factorial,
etcetera. All the way down the line, one never stops this sum; keeps going forever and ever.
Now recall that k factorial for a positive integer k is defined to be, k times k minus 1 times k minus 2, and all
the way down until you get to 3 times 2 times 1.
That gives the sequence of numbers that we saw at the beginning. Recall also that by convention and for
very good reasons, 0 factorial is defined to be 1. Thus we could write our definition for e to the x using summation notation. As the sum k goes from 0 to infinity of x to the k divided by k factorial.
Well, definitions may be nice, but what do we do with it? How do we deal with this statement? How do we even make sense of this infinite sum.
Well, certainly for specific values of x, say x equal to 1, we can try to compute what e to the one would be, as plus one plus one half plus one sixth plus one 24th, etcetera. It seems as though this converges to the
familiar decimal expansion for e that we know.
In general, the principle that you should follow in trying to understand statements such as the definition of e to the x is to pretend that this is a long polynomial; a polynomial of unbounded degree. Now, polynomials are wonderful objects to work with, very simple from the point of view of differential and integral calculus.
Recall that when it comes to differentiation, the derivative of x to the k is k times x to the k minus one. Likewise the integral of x to the k is x to the k plus one over k plus one. Don't forget the arbitrary constant, and don't forget that something unusual happens when k is equal to negative one. Both of these properties, should be familiar from your previous exposure to calculus.
Given these facts about polynomials, let's see what we can observe about e to the x. For example, if we tried to differentiate e to the x by using our definition, then what would we obtain? Well, thinking of u to the x as a long polynomial in x, allows us to apply what we already know. For example, what is the derivative of one? That's clearing zero.
The derivative of x is clearly 1. What is the derivative of 1 over 2 factoral times x squared. Well, it's 1 over 2 factorial times the derivative of x squared, which is 2x. We can continue on down the line, taking the derivative of x cubed, to be 3x squared. Following the constants as we go. Now a little bit of simplification tells us that the 2x divided by 2 factorial gives us simply x. The 3x squared divided by 3 factorial gives us simply x squared over 2 factorial.
This pattern continues since k divided by k factorial is one over quantity k minus one factorial. And what do we observe? We observe that we obtain the definition of e to the x by simply following what seemed to be the obvious thing to do.
Will that work if we try to integrate as well? Let's see. If we try to integrate our definition, v to the x. 1 plus x plus x squared over 2, etcetera. What will we get? While the integral of 1 gives us x, the integral of x gives us one half x squared. If we have a 1 over 2 factorial times the integral of x squared, that's 1 3rd x cubed.
Now, I'll let you follow this pattern all the way down the line, and see that with a little bit of simplification, we wind up getting, not quite e to the x. It appears as though, we're missing the first term. We're missing the 1 out in front. So now, we've obtained e to the x minus 1, that's not quite the way I remember the integral of e to the x going.
However, we have forgotten as one often does, the arbitrary constant out in front. We could absorb that negative 1 into the arbitrary constant, and what we've obtained is up to a constant e to the x.
We'll recall Euler's formula that tells us something about exponentiating i times x in terms of cosines and sines. What happens if we apply our definition of the exponential in this case. If we want to take e to the i times x.
Well, this is 1 plus i times x, plus 1 over 2 factorial times quantity ix squared. That is, i squared times x squared etcetera, etcetera. There are a lot of terms here.
Then it appears as though there are some simplifications that we can do. Recall that by definition, i squared and the square root of negative 1 squared, must be negative 1. Therefore, if we look at i cubed, we have
to get negative i. And i to the fourth, being i squared, squared, must be equal to 1. Therefore, we have a sick-lick pattern in our powers of i that allows us to simplify this expression as 1 plus ix minus x squared over 2 factorial, minus ix cubed over 3 factorial plus x to the fourth over 4 factorial etcetera. You can see the pluses and the minuses coming in alternating pairs, and the real versus imaginary terms alternating with each term.
Now, if we were to do what we do when we work with complex numbers and collect all of the real terms into one part, and all of the imaginary terms into the other then what would we obtain? Well, the real portion of this expression is, 1 minus x squared over 2 factorial, plus x to the fourth over 4 factorial, etcetera.
With the signs alternating and with even powers of x. From Euler's formula, that must be the cosine of x.
Likewise, the sin of x must be the imaginary portion of this expression. That is, x minus x cubed over 3 factorial, plus x to the fifth over 5 factorial, etcetera. With odd powers and alternating signs.
Our conclusion from this rather simplistic manipulation is, that we now have alternate expressions for certain
trigonometric functions. The cosine of x is 1 minus x squared over 2 factorial plus x to the fourth over 4 factorial minus x to the sixth over 6 factorial, etcetera. In summation notation, we can use a wonderful little trick to express this compactly, as the sum k goes from 0 to infinity of negative 1 to the k times x to the 2k over quantity 2k factorial.
That builds in the alternating signs and the even powers. Likewise, for sine of x, we can write this in a summation notation, with a similar idea as the sum k goes from 0 to infinity of negative 1 to the k times x
to the 2k plus 1 over quantity 2k plus 1 factorial. This gives us the odd powers of x.
Now, you may recall that the trigonometric functions have some very nice properties, with respect to calculus.
For example, you may remember something about the derivative sign of x. Let's see what happens, when we take our newly derived expression and differentiate it, as if it were the long polynomial. The derivative of x is 1. The derivative of x cubed is 3x squared, we must divide this by 3 factorial. The derivative of x to the fifth and x to the seventh follow the familiar pattern with a little bit of cancellation of the coefficents, what do we see?
Well, we get 1 minus x squared over 2 factorial, plus x to the fourth over 4 factorial, minus x to the sixth over 6 factorial, etcetera. This is an expression that we have very recently seen. this is out derived expression for the cosine of x. And you may recall that the derivative of sine is cosine. But without any complicated proof, we've derived this expression very simply, by pretending that everything in sight is a long polynomial.
factorial notation. That e to the x is 1 + x + x squared over 2 factorial + x cubed over 3 factorial,
etcetera. All the way down the line, one never stops this sum; keeps going forever and ever.
Now recall that k factorial for a positive integer k is defined to be, k times k minus 1 times k minus 2, and all
the way down until you get to 3 times 2 times 1.
That gives the sequence of numbers that we saw at the beginning. Recall also that by convention and for
very good reasons, 0 factorial is defined to be 1. Thus we could write our definition for e to the x using summation notation. As the sum k goes from 0 to infinity of x to the k divided by k factorial.
Well, certainly for specific values of x, say x equal to 1, we can try to compute what e to the one would be, as plus one plus one half plus one sixth plus one 24th, etcetera. It seems as though this converges to the
familiar decimal expansion for e that we know.
In general, the principle that you should follow in trying to understand statements such as the definition of e to the x is to pretend that this is a long polynomial; a polynomial of unbounded degree. Now, polynomials are wonderful objects to work with, very simple from the point of view of differential and integral calculus.
Recall that when it comes to differentiation, the derivative of x to the k is k times x to the k minus one. Likewise the integral of x to the k is x to the k plus one over k plus one. Don't forget the arbitrary constant, and don't forget that something unusual happens when k is equal to negative one. Both of these properties, should be familiar from your previous exposure to calculus.
Given these facts about polynomials, let's see what we can observe about e to the x. For example, if we tried to differentiate e to the x by using our definition, then what would we obtain? Well, thinking of u to the x as a long polynomial in x, allows us to apply what we already know. For example, what is the derivative of one? That's clearing zero.
The derivative of x is clearly 1. What is the derivative of 1 over 2 factoral times x squared. Well, it's 1 over 2 factorial times the derivative of x squared, which is 2x. We can continue on down the line, taking the derivative of x cubed, to be 3x squared. Following the constants as we go. Now a little bit of simplification tells us that the 2x divided by 2 factorial gives us simply x. The 3x squared divided by 3 factorial gives us simply x squared over 2 factorial.
This pattern continues since k divided by k factorial is one over quantity k minus one factorial. And what do we observe? We observe that we obtain the definition of e to the x by simply following what seemed to be the obvious thing to do.
Now, I'll let you follow this pattern all the way down the line, and see that with a little bit of simplification, we wind up getting, not quite e to the x. It appears as though, we're missing the first term. We're missing the 1 out in front. So now, we've obtained e to the x minus 1, that's not quite the way I remember the integral of e to the x going.
However, we have forgotten as one often does, the arbitrary constant out in front. We could absorb that negative 1 into the arbitrary constant, and what we've obtained is up to a constant e to the x.
Well, this is 1 plus i times x, plus 1 over 2 factorial times quantity ix squared. That is, i squared times x squared etcetera, etcetera. There are a lot of terms here.
Then it appears as though there are some simplifications that we can do. Recall that by definition, i squared and the square root of negative 1 squared, must be negative 1. Therefore, if we look at i cubed, we have
to get negative i. And i to the fourth, being i squared, squared, must be equal to 1. Therefore, we have a sick-lick pattern in our powers of i that allows us to simplify this expression as 1 plus ix minus x squared over 2 factorial, minus ix cubed over 3 factorial plus x to the fourth over 4 factorial etcetera. You can see the pluses and the minuses coming in alternating pairs, and the real versus imaginary terms alternating with each term.
Now, if we were to do what we do when we work with complex numbers and collect all of the real terms into one part, and all of the imaginary terms into the other then what would we obtain? Well, the real portion of this expression is, 1 minus x squared over 2 factorial, plus x to the fourth over 4 factorial, etcetera.
With the signs alternating and with even powers of x. From Euler's formula, that must be the cosine of x.
Likewise, the sin of x must be the imaginary portion of this expression. That is, x minus x cubed over 3 factorial, plus x to the fifth over 5 factorial, etcetera. With odd powers and alternating signs.
trigonometric functions. The cosine of x is 1 minus x squared over 2 factorial plus x to the fourth over 4 factorial minus x to the sixth over 6 factorial, etcetera. In summation notation, we can use a wonderful little trick to express this compactly, as the sum k goes from 0 to infinity of negative 1 to the k times x to the 2k over quantity 2k factorial.
That builds in the alternating signs and the even powers. Likewise, for sine of x, we can write this in a summation notation, with a similar idea as the sum k goes from 0 to infinity of negative 1 to the k times x
to the 2k plus 1 over quantity 2k plus 1 factorial. This gives us the odd powers of x.
Now, you may recall that the trigonometric functions have some very nice properties, with respect to calculus.
Well, we get 1 minus x squared over 2 factorial, plus x to the fourth over 4 factorial, minus x to the sixth over 6 factorial, etcetera. This is an expression that we have very recently seen. this is out derived expression for the cosine of x. And you may recall that the derivative of sine is cosine. But without any complicated proof, we've derived this expression very simply, by pretending that everything in sight is a long polynomial.
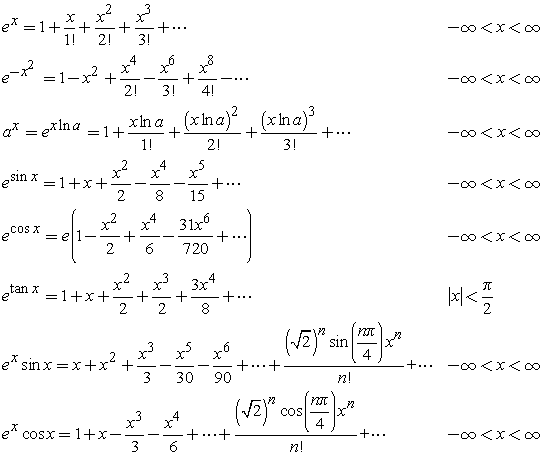
Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου